WebShapes

About WebShapes

WebShapes is a web platform that provides users the possibility to create various network shapes with different methods and parameters, where users can upload their own networks and download the shape information for analysis.

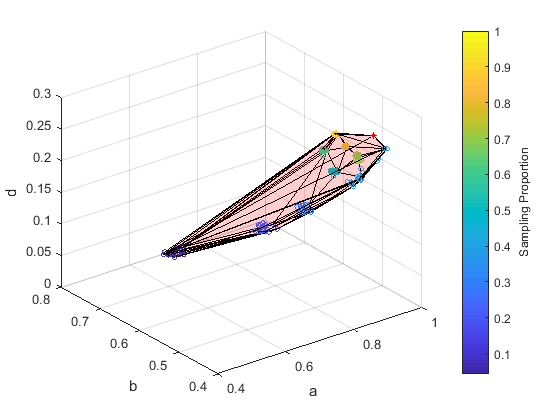
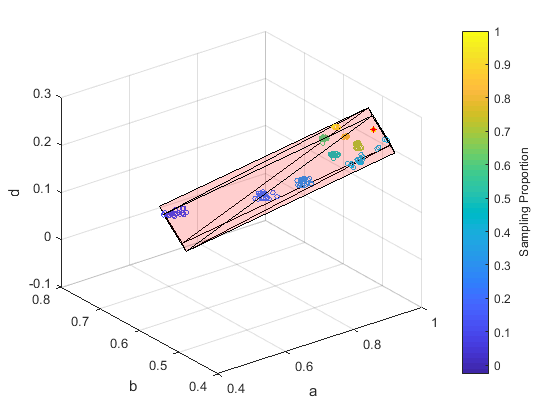
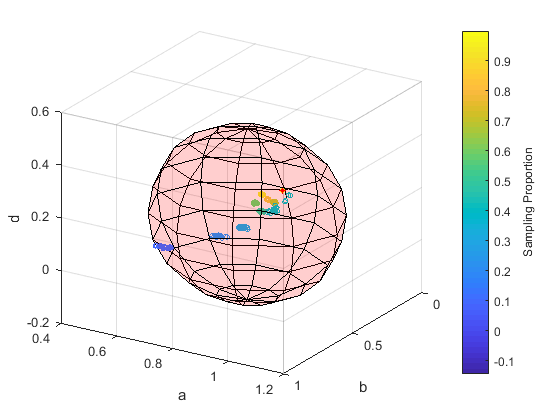
Network Shapes is a method to represent any network with a 3D shape. Shapes capture various network properties: isomorphic graphs = same shapes, different graphs (random graphs, dense graphs, etc.) have different shapes. The following simple steps can help build a network shape:

Step 1: Sample many subgraphs from the network

Step 2: Map the network and its subgraphs to 3D vectors

Step 3: Fit a 3D Shape to the set of 3D vectors

Theoretically, any graph sampling strategy, graph embedding method and fitting method can be used in these three steps to build a network shape. This web application allows researchers to quicly build and visualize a customized network shape. In order to get going, hit the "Try It Now" button. All you need to do is choose a network to build a shape, and you can download the figure and information (such as the boundary points) of the shape.

For more details, please refer to Jin, Shengmin, and Reza Zafarani. "Representing Networks with 3D Shapes." 2018 IEEE International Conference on Data Mining (ICDM). IEEE, 2018.https://shengminjin.github.io/files/NetworkShapes.pdf.

In the rest of this page, we have a brief introduction to the graph sampling strategies, graph embedding methods and fitting methods currently supported by this web application WebShapes.

How to Use WebShapes

1. Select the parameters (e.g., sampling method, the embedding method...);

2. Select a pre-existing dataset, or upload your own dataset (a tab delimitered edgelist file, one can download the example file through the example link);

3. After choosing (or uploading) the dataset, click the "Visualize" button, and it may take some time to create a network shape based on the network size and number of samples (a network like as20graph can take about 3 minutes; for very large networks it can take hours);

4. The shape figure will be illustrated on the web browser when it finishes;

5. One can click the "Download" button to download the files (the figure, boundary points...).

Sampling Types

Random Node

Select a set of nodes at uniformly random and take the graph induced by the selected nodes as a sample.

Random Walk

Select a set of edges uniformly at random and take the graph induced by the selected edges as a sample.

Random Edge

Pick a starting node uniformly at random and then simulate a random walk on the graph. At every step with probability, we fly back to the starting node and re-start the random walk.

Embedding Types

Kronecker Point Embedding

Kronecker Point is used to embed an undirected network, or any of its subgraphs, to a point (a,b,d) in the 3D space using Stochastic Kronecker Graphs. Values a, b and d are in range [0,1].

graph2vec

graph2vec views a graph as a document and the rooted subgraphs around each node as words. It extends document embedding neural networks to learn vector representations of entire graphs.

Fitting Types

Convex Hull

A convex hull is the smallest convex set that contains all the points in the original set. To save a convex hull, one can save its boundary points.

Cuboid

We compute the minimal box (with right angles) around the points. To save the 3D cuboid, we save the 8 extreme points.

Sphere

We compute the centroid (the arithmetic mean position) of the points as the center, and use the longest distance from the points to the origin as the diameter. To save a sphere, one can save the center and the radius.